Vectors
Vector intro for linear algebra
What is a Vector?
- A vector has both magnitude (size) and direction.
- Example:
- Not a vector: "Moving at 5 miles per hour" (only magnitude).
- Vector: "Moving at 5 miles per hour east" (magnitude + direction).
- Speed is a scalar (only magnitude), while velocity is a vector (magnitude + direction).
Visualizing a Vector
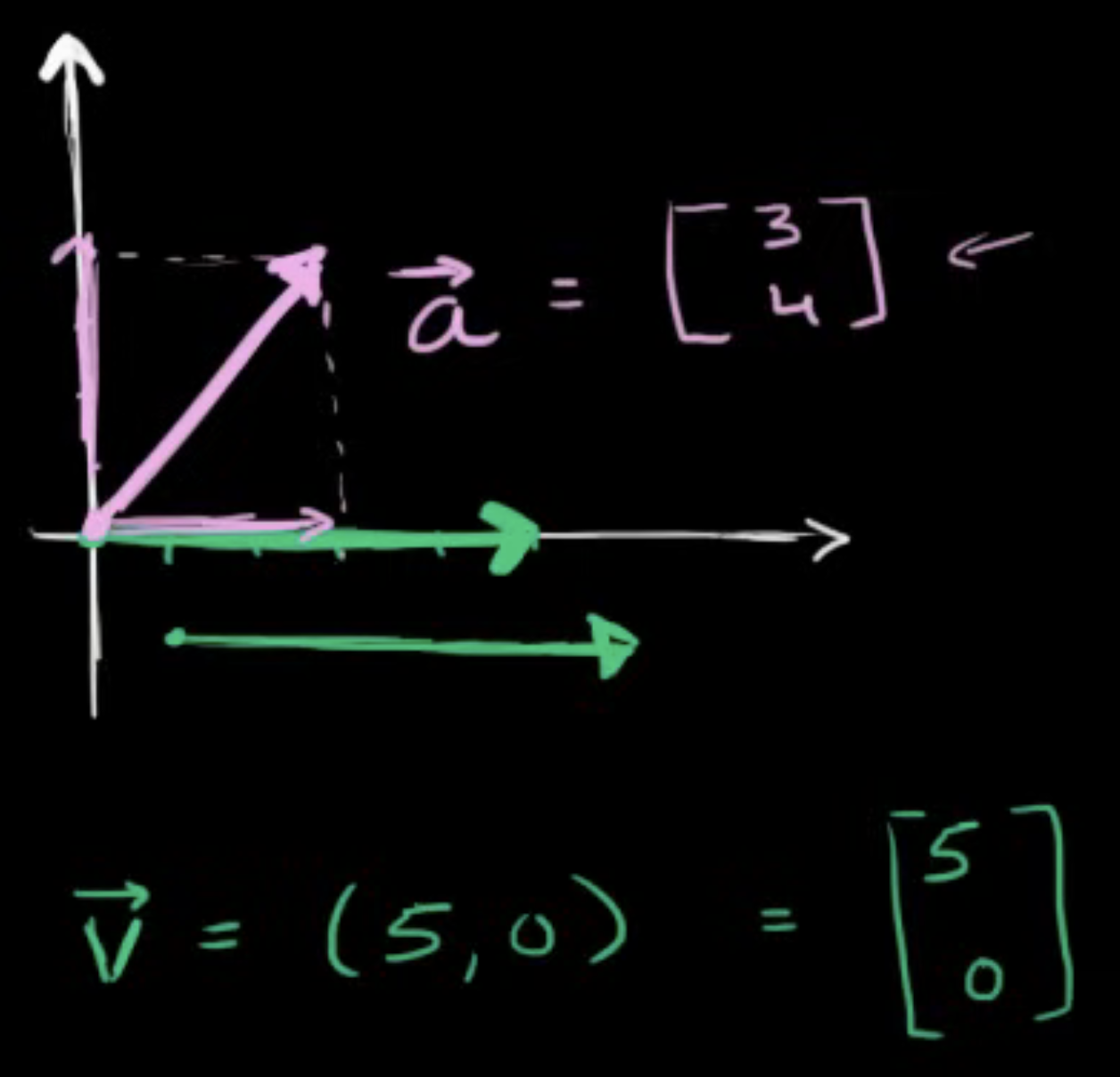
- A vector can be represented as an arrow:
- Arrow length = magnitude of the vector.
- Arrow direction = direction of the vector.
- Vectors can be moved around if they keep the same magnitude and direction.
Vector Representation in 2D
- In two dimensions, a vector is written as (x, y):
- The first value (x) represents movement in the horizontal direction.
- The second value (y) represents movement in the vertical direction.
- Example:
- A vector v moving 5 units east: (5, 0)
- A vector a moving 3 right and 4 up: (3, 4)
Column Vector Notation
- Instead of writing as a row (x, y), vectors are often written as column vectors:
[ 5 ]
[ 0 ]
- This format is widely used in linear algebra.
Magnitude of a Vector
- The length of a vector can be found using the Pythagorean theorem:
- For a vector (3, 4):
Magnitude = √(3² + 4²) = √9 + 16 = √25 = 5 - This is useful in determining the size of a vector.
Extending Vectors to Higher Dimensions
- Linear algebra allows working with vectors in 3D, 4D, or even higher dimensions.
- While we can visualize up to 3D, mathematical notation helps work with higher dimensions.
Real coordinate spaces
What is R² (Two-Dimensional Real Coordinate Space)?
- Notation: R² (or ℝ²) represents two-dimensional real coordinate space.
- Meaning: It includes all possible ordered pairs (x, y) of real numbers.
- Example:
- A vector (3,4) belongs to R².
- A vector (4,3) is different from (3,4) because order matters.
- Visual Representation:
- Vectors in R² can be represented as arrows in a 2D coordinate plane.
- Example: The vector (4,3) moves 4 units right and 3 units up.
What is a Tuple?
- A tuple is an ordered list of numbers.
- A 2-tuple is an ordered pair (x, y).
- In R², all numbers in the tuple must be real numbers (no imaginary numbers).
- Example:
- (3,4) and (-3,-4) are both in R².
- (i, 2) is not in R² because i is imaginary.
What is R³ (Three-Dimensional Real Coordinate Space)?
- Notation: R³ (or ℝ³) represents three-dimensional real coordinate space.
- Meaning: It includes all possible ordered triplets (x, y, z) of real numbers.
- Example:
- A vector (2, -1, 4) belongs to R³.
- A vector (-1, 5, 3) is also in R³.
- Visual Representation:
- Vectors in R³ can be drawn in a 3D coordinate system with x, y, and z axes.
What is Rⁿ (Higher-Dimensional Real Coordinate Space)?
- Notation: Rⁿ (or ℝⁿ) represents n-dimensional real coordinate space.
- Meaning: It includes all possible ordered n-tuples (x₁, x₂, ..., xₙ) of real numbers.
- Example:
- A 4D vector (1,2,3,4) is in R⁴.
- A 100D vector (x₁, x₂, ..., x₁₀₀) is in R¹⁰⁰.
- Visualization:
- R³ is easy to visualize.
- R⁴ and beyond cannot be visualized, but can be represented mathematically.
What is NOT in Rⁿ?
- A vector with fewer dimensions is not in a higher-dimensional space:
- Example: (3,4) is in R², but not in R³.
- A vector with imaginary numbers is not in Rⁿ:
- Example: (i, 2, 3) is not in R³ because i is imaginary.
Adding vectors algebraically & graphically
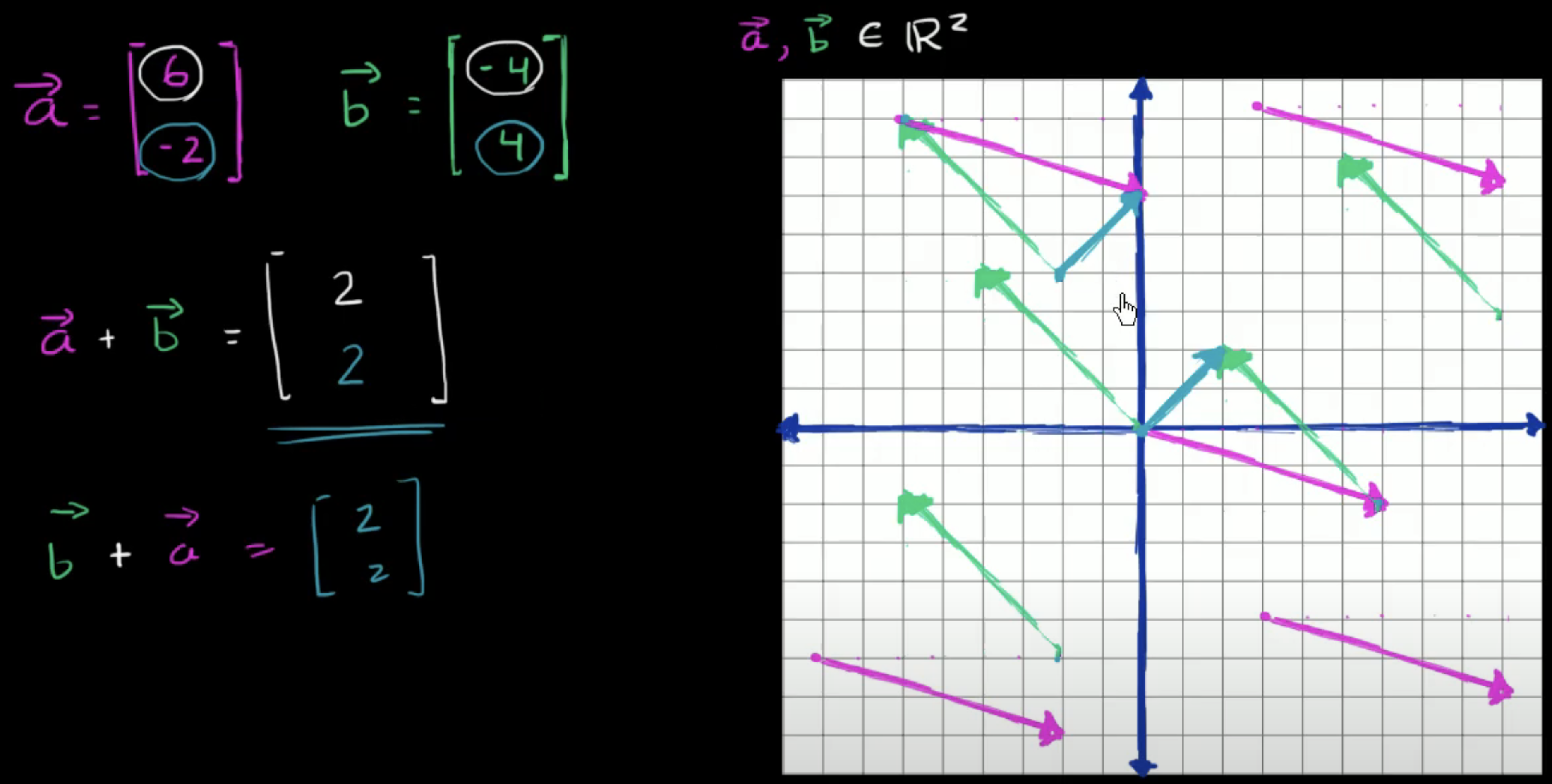
1. Definition of Vector Addition
- Given two 2D vectors, a and b, we define their sum by adding corresponding components:
- If a = (6, -2) and b = (-4, 4):
- First component: 6 + (-4) = 2
- Second component: -2 + 4 = 2
- So, a + b = (2,2).
- If a = (6, -2) and b = (-4, 4):
2. Visual Representation of Vector Addition
- Vectors are represented as arrows on the coordinate plane.
- Magnitude (length of the arrow) and direction define a vector.
- A vector can be moved if its magnitude and direction remain unchanged.
3. Step-by-Step Visual Addition of Vectors
- Draw vector a starting from the origin.
- Draw vector b starting from the origin (or at the head of vector a).
- The resultant vector (sum) is the vector that starts at the origin and ends at the tip of the second vector.
4. The "Tip-to-Tail" Method
- To add a + b:
- Start with vector a from the origin.
- Place vector b at the head of vector a.
- Draw the resultant vector from the origin to the tip of b.
- The same works for b + a, proving that vector addition is commutative.
5. Commutative Property of Vector Addition
- a + b = b + a:
- Numerically, adding components in any order gives the same result.
- Visually, switching the order of the vectors still results in the same resultant vector.
6. Conceptual Understanding
- Vector addition represents combined movement or shift in space.
- It applies to:
- Displacement (movement in space).
- Velocity (combining speeds in different directions).
- Acceleration (combining forces acting on an object).
- The sum represents the overall effect of two vectors combined.