Two Pointers: Cycle Finding
Linked List Cycle II
This question is the same as Linked List Cycle,
except in addition to checking whether a linked list has a loop,
we also find the size of the loop, if applicable.
Parameters
nodes: The first node of a linked list with potentially a loop.
Result
An integer representing the size of the loop, if there is one. If there is no loop, output -1.
Example 1
Input: 0 -> 1 -> 2 -> 3 -> 4
^ |
|_ _ _ _ _ _ _
Output: 4 (there is a loop of size 4, starting from node 1)
Example 2
Input: 0 -> 1 -> 2 -> 3 -> 4
Output: -1 (there is no loop)
Constraints
1 <= len(nodes) <= 10^5
class Node {
constructor(val, next=Null) {
this.val = val;
this.next = next;
}
}
function nodeNext(node) {
return node.next || node;
}
function cycleSize(nodes) {
let tortoise = nodeNext(nodes);
let hare = nodeNext(nodeNext(nodes));
while (tortoise !== hare && hare.next) {
tortoise = nodeNext(tortoise);
hare = nodeNext(nodeNext(hare));
}
if (!hare.next) return -1;
let count = 1;
tortoise = nodeNext(tortoise);
hare = nodeNext(nodeNext(hare));
while (tortoise !== hare) {
count++;
tortoise = nodeNext(tortoise);
hare = nodeNext(nodeNext(hare));
}
return count;
}
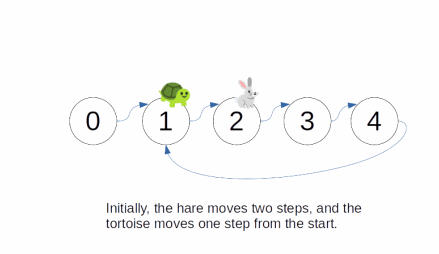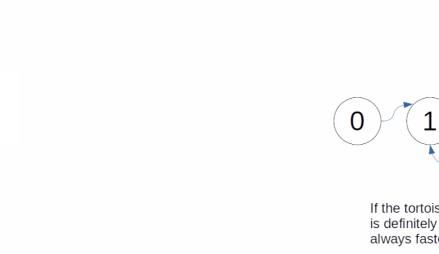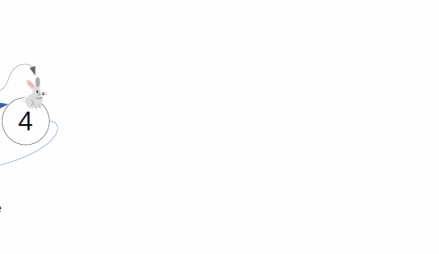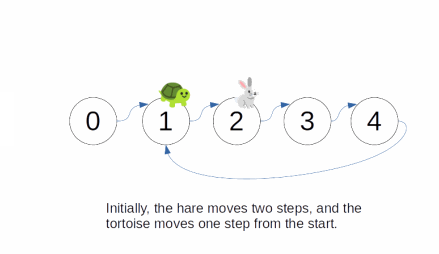
Explanation
- The basic idea is the same as in Linked List Cycle, except how do we determine the size of the loop?
- Let's say that the loop size is r and the tortoise and the hare already met up
- They must both be inside the loop, otherwise they cannot be at the same location
- Let's say that after k cycle, they meet up again
- In that case, k % r == 2k % r, which means that k % r == 0
- The smallest k where this is possible is when k == r
- This means that after they meet, we start counting the number of cycles that passed until they meet again
- Then, that must be the size of the cycle
- Time Complexity:
O(n)