Backtracking: Memoization
Word Break
Given a string and a list of words, determine if the string can be constructed from concatenating words from the list of words.
A word can be used multiple times.
Example 1:
Input:
s = "algomonster"
words = ["algo", "monster"]
Output: true
Example 2:
Input:
s = "aab"
words = ["a", "c"]
Output: false
- Solution 1
function wordBreak(s, words) {
return dfs(s, words, []);
}
function dfs(s, words, path) {
let result = false;
let wordsStr = path.join("");
if (wordsStr === s) return true;
if (wordsStr.length >= s.length) return false;
for (const word of words) {
path.push(word);
result = dfs(s, words, path);
if (result) break;
path.pop();
}
return result;
}
- Solution 2
function wordBreak(s, words) {
return dfs(s, words, 0);
}
function dfs(s, words, i) {
// we have constructed the entire target s
if (i === s.length) return true;
for (const word of words) {
if (s.slice(i).startsWith(word)) {
// is this a valid path
if (dfs(s, words, i + word.length)) return true; // any path leads to true is fine
}
}
return false;
}
- Solution 3:
function wordBreak(s, words, start = 0, memo = []) {
if (start === s.length) return true;
if (memo[start] !== undefined) return memo[start];
for (let i = 0, len = s.length; i + start <= len; i++) {
if (
words.indexOf(s.substr(start, i)) > -1 &&
wordBreak(s, words, i + start, memo)
) {
return (memo[start] = true);
}
}
return (memo[start] = false);
}
- Solution 4: using memoization
function wordBreak(s, words) {
return dfs(s, words, 0, {});
}
function dfs(s, words, i, memo) {
if (i === s.length) return true;
if (i in memo) return memo[i];
let result = false;
for (const word of words) {
if (s.slice(i).startsWith(word)) {
if (dfs(s, words, i + word.length, memo)) {
result = true;
break;
}
}
}
memo[i] = result;
return result;
}
Explanation
- This is yet another combinatorial search problem. Let's apply the three-step backtracking system
-
Identify the states
- To determine whether we have completely constructed target s, we have to find
- What are the characters left to be matched using words in the list
- To make a choice when we visit the current node's children
- we don't need any additional states since we can use any word in the list unlimited times
- To determine whether we have completely constructed target s, we have to find
-
Draw the space-state tree
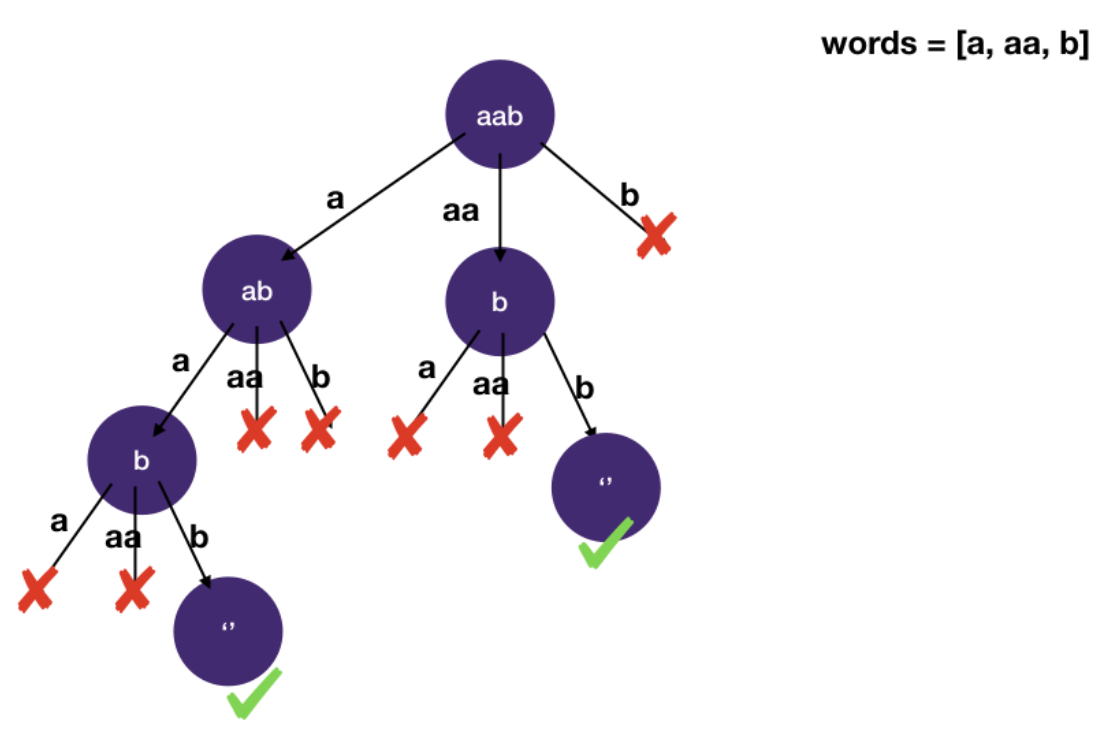
- Note that in the above figure, there are two paths that lead to an empty string
- i.e. completely matching target
- When we DFS we would reach the left one first without visiting the other one since we just need one successful path to return true
- Note that in the above figure, there are two paths that lead to an empty string
-
DFS on the space-state tree
- Using the backtracking template as a basis, we add the state we identified in step 1:
- We use index i to record the current position in the target we have matched so far
- s[:i] is matched and s[i:] is to be matched
- We use index i to record the current position in the target we have matched so far
- Using the backtracking template as a basis, we add the state we identified in step 1:
Memoization
-
Everything looks great. When we finish typing that last bracket/semicolon
- we can almost hear angels singing and all tests passing
-
Except there is one pesky test case
"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab"
["a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa","aaaaaaaaa","aaaaaaaaaa"] -
Why does this one time out?
- We have 10 branches to check each level of the tree and there are 140 as in the target
- in the worse case we'd be looking at 10^140 branches
- Remember we talked about "combinatorial explosion" in the backtracking module
- We have just been struck by it
- The way to solve this is to use memoization to cache the branches we have already seen
- We can even see duplicate in the above example
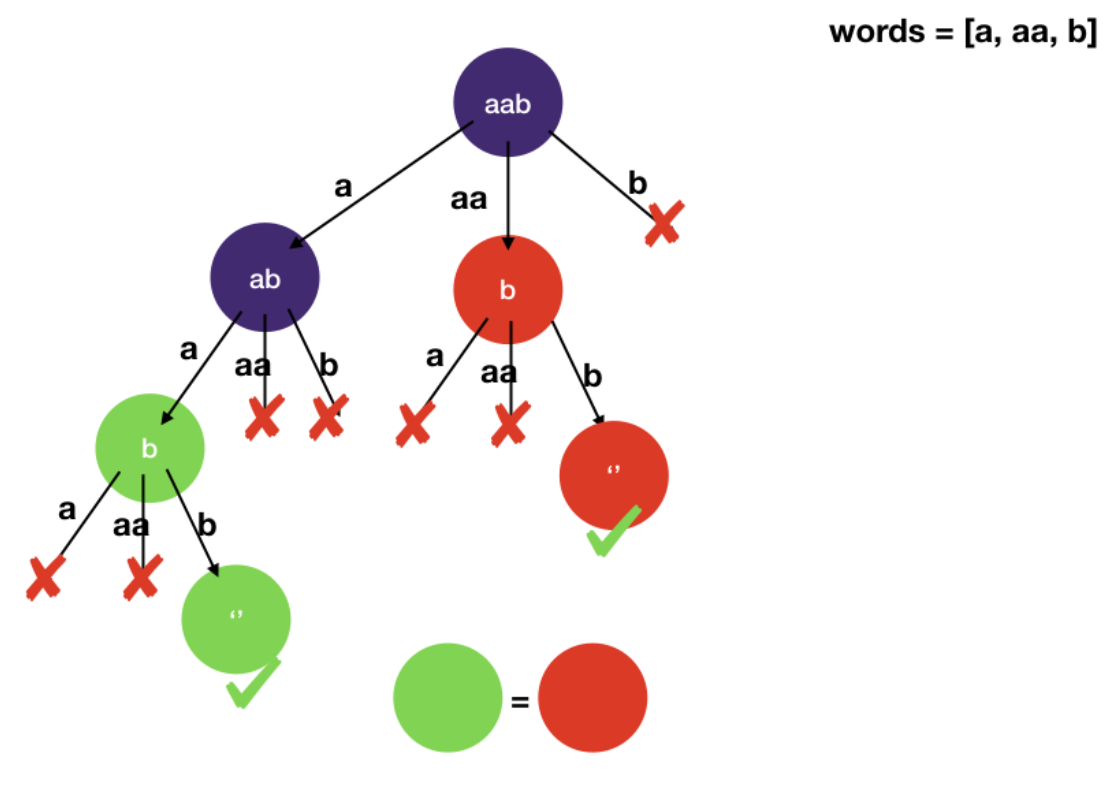
- We have 10 branches to check each level of the tree and there are 140 as in the target
-
Time Complexity:
O(s * w * max(w[i])) -
s is the length of the string, w is the length of the words array and max(w[i]) is the maximal possible word length
- Here our time complexity is polynomial since we memoize and we iterate through the possibilities
- At every position s we try every word in w which takes time proportionate to the word length