Backtracking
Combinatorial Search pattern
- Combinatorial search problems involve finding grouping and assignments of objects that satisfy certain conditions
- Finding all permutations/subsets, solving sudoku, and 8-queens are classic combinatorial problems
Permutations
- permutation means arranging things with an order
- i.e. permutation of
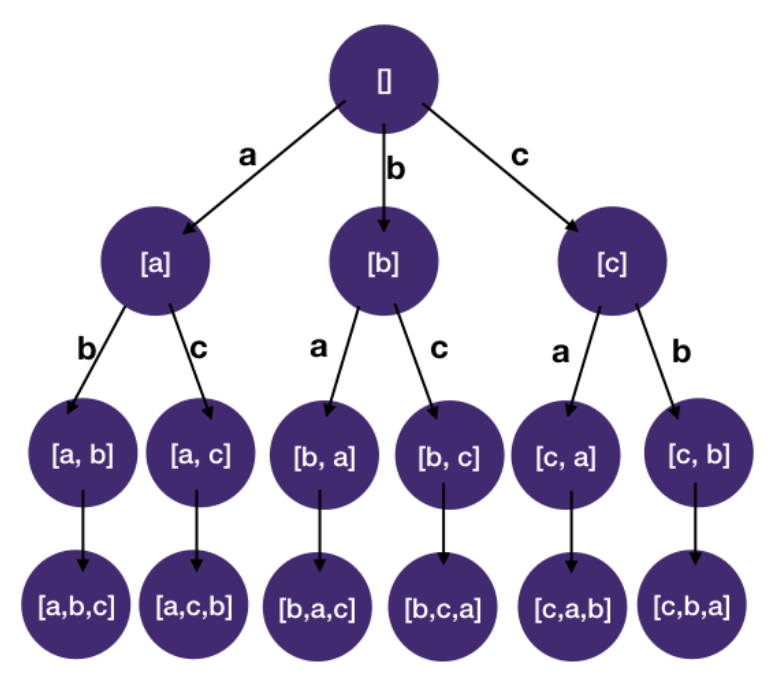
[a, b, c]is[a, b, c],[a, c, b],[b, a, c],[b, c, a],[c, a, b],[c, b, a]
- i.e. permutation of
- important to review basic high school combinatorics to get an intuition for combinatorial problems
- The number of permutations is given by
n! - i.e. a bag of 3 letters, total number of choices is
3 * 2 * 1 = 6, have 6 leaf nodes in a tree
Complexity
- The complexity of combinatorial problems often grows rapidly with the size of the problem
- i.e. the number of permutation of 3 objects is only 6
- However, number of permutation of 10 objects is about 3 million
- The number of permutations of 11 objects is about 40 million
- The rapid growth of solution space with even a small increase in problem size is called
combinatorial explosion
- i.e. the number of permutation of 3 objects is only 6
Combinatorial search == DFS on tree
- In combinatorial search problems, search space is in the shape of a tree
- The tree that represents all the possible states is called a
State-space Tree - Each node of the
state-space treerepresents a state we can reach in a combinatorial search (by doing a particular combination)- Leaf nodes are the solutions to the problem
- Combinatorial search problems boil down to DFS / backtracking on the
state-space tree - Since the search space can be quite large, we often have to
prunethe tree- i.e. discard branches
Three steps to conquer combinatorial search problems
-
Identify the state(s)
- we want to answer the following 2 questions to identify the states
- What state do we need to know whether we have reached a solution (and using it to construct a solution if the problem asks for it)
- i.e. we keep track of the letters we have already selected when we do DFS for
[a, b, c]example
- i.e. we keep track of the letters we have already selected when we do DFS for
- What state do we need to decide which child nodes should be visited next and which ones should be pruned
- i.e. we have to know what are the letters left that we can still use (since each letter can only be used once) for
[a, b, c]example
- i.e. we have to know what are the letters left that we can still use (since each letter can only be used once) for
- What state do we need to know whether we have reached a solution (and using it to construct a solution if the problem asks for it)
- we want to answer the following 2 questions to identify the states
-
Draw the state-space tree
- you want to draw the tree (on a piece of paper if you have one)
- A small test case that's big enough to reach one solution (leaf node)
- after drawing the tree, simply traverse the tree depth-first
-
DFS / backtrack on the state-space tree
- apply the following
backtracking template
function dfs(node, state):
if state is a solution:
report(state) # e.g. add state to final result list
return
for child in children:
if child is a part of a potential solution:
state.add(child) # make move
dfs(child, state)
state.remove(child) # backtrack - apply the following
- unlike the following
Ternary Tree Pathsexample which has an explicit tree, in combinatorial search problems we have to find our own tree
DFS with states
Ternary Tree Paths
- each node of the tree has at most three children, find all root-to-leaf paths
- use path to keep track of the nodes we have visited to reach the current node and use it to construct our solution when we reach leaf nodes
Javascript
class Node {
constructor(val, children = []) {
this.val = val;
this.children = children;
}
}
function dfs(root, path, res) {
// exit condition, reached leaf node, append paths to results
if (root.children.length === 0) {
path.push(root.val); // add current node value to path if children is null
res.push(path.join("->"));
path.pop(); // remove recent add node value from path
return;
}
// dfs on each non-null child
for (const child of root.children) {
if (child) {
path.push(root.val); // add current node value to path if children exist
dfs(child, path, res);
path.pop();
}
}
}
function ternaryTreePaths(root) {
let res = [];
if (root) dfs(root, [], res);
return res;
}
const one = new Node(1);
const two = new Node(2);
const four = new Node(4);
const six = new Node(6);
const three = new Node(3);
one.children = [two, four, six];
two.children = [three];
const result = ternaryTreePaths(one);
console.log(result);
Memoization pattern
- It means saving the previous function call result in a dictionary and reading from it when we do the exact same call
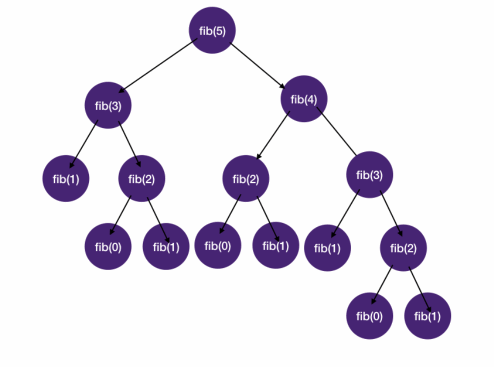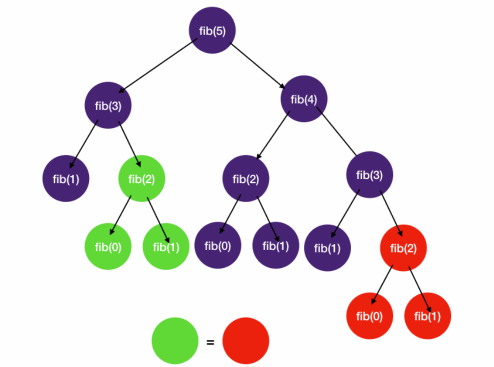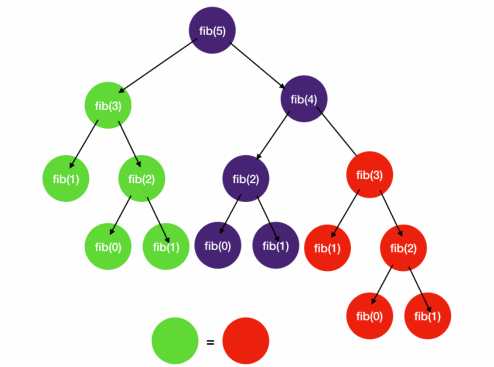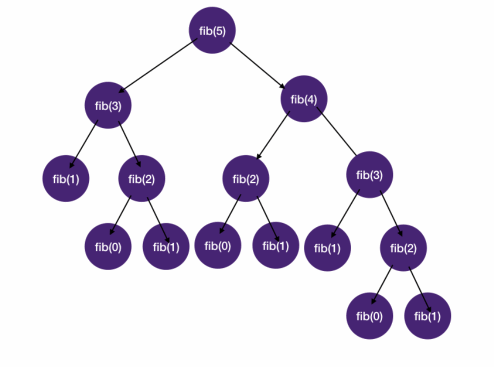
- Memoization is particularly useful for combinatorial problems that have large repeated state-space tree branches
without memoization results in a lot of repeated computations
Javascript
function fib(n) {
if (n === 0 || n === 1) {
return n;
}
return fib(n - 1) + fib(n - 2);
}
with memoization
- The solution is saving previous results in a map of function argument to results (the "memo")
- and checking it and returning previous results if it has been done before
- Otherwise, we carry out the computation and save the results in the map
Javascript
function fib(n, memo = {}) {
// check in memo, if found, retrieve and return right away
if (n in memo) return memo[n];
if (n === 0 || n === 1) return n;
const res = fib(n - 1, memo) + fib(n - 2, memo);
// save result to memo before returning
memo[n] = res;
return res;
}
Pruning pattern
- cut branches off the space-state tree
- The fewer branches, the faster the algorithm
- When do we want to prune a branch? When it's clear that going into that branch would not yield a final state