Graph pattern
Fundamentals
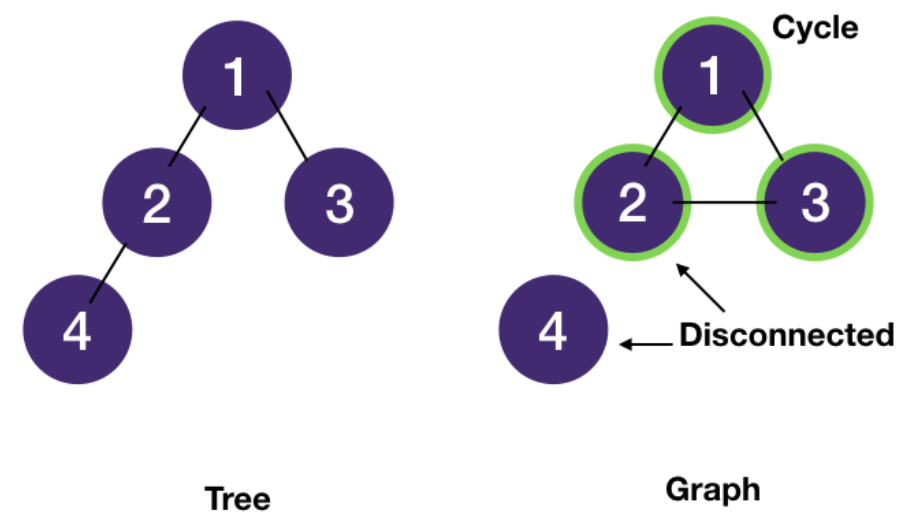
Tree with 0+ cycle
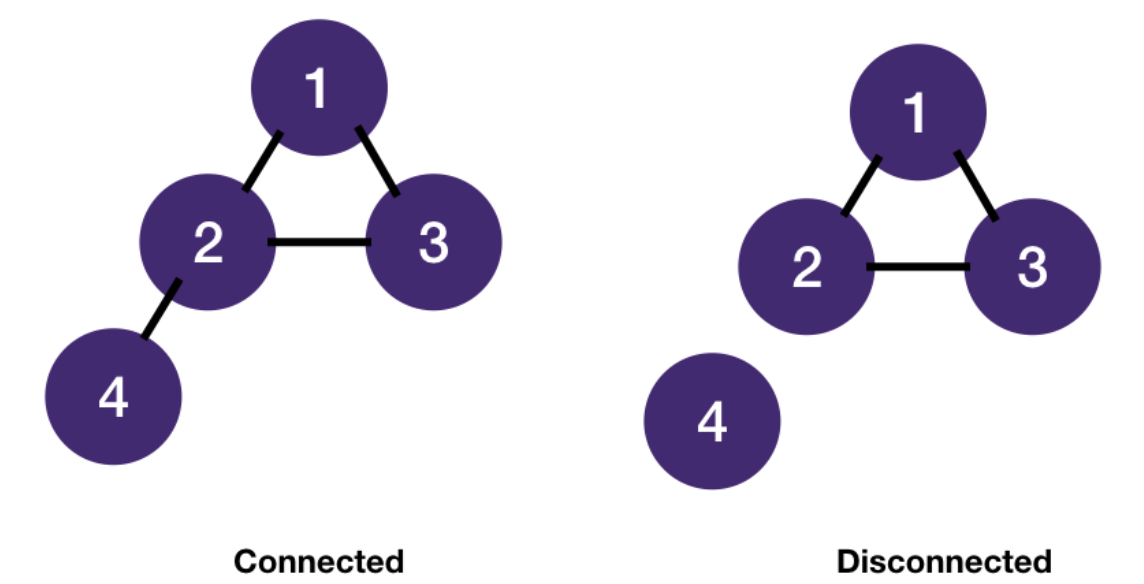
- A tree is a special graph - a connected acyclic (cycle-less) graph.
- A graph may contain cycle(s) and nodes could be disconnected.
- A tree also contains n nodes and n - 1 edges in addition to being acyclic and there exists only 1 path between 2 nodes in a tree.
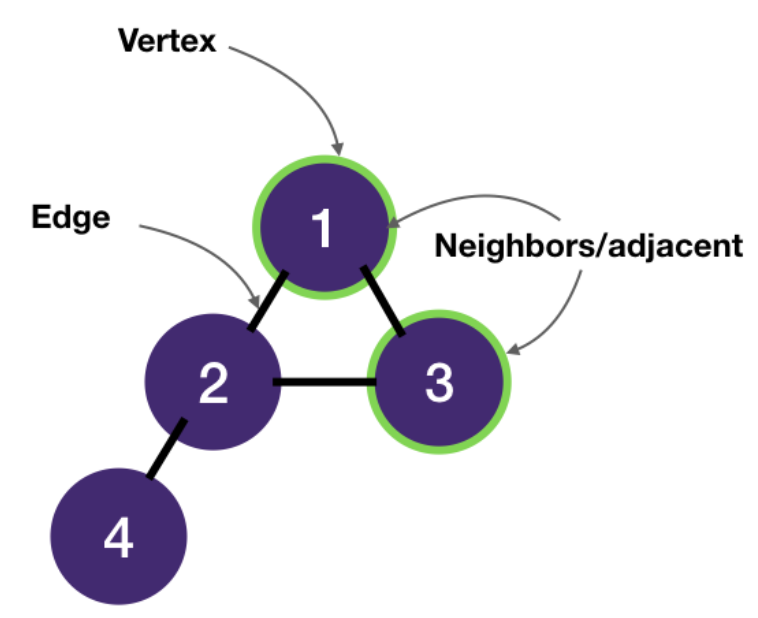
Graph Terminologies
- A graph consists of vertices ("nodes" in trees) and edges.
- Vertices are connected by edges.
- Two vertices connected by an edge are called neighbors and are adjacent ("children" in trees).
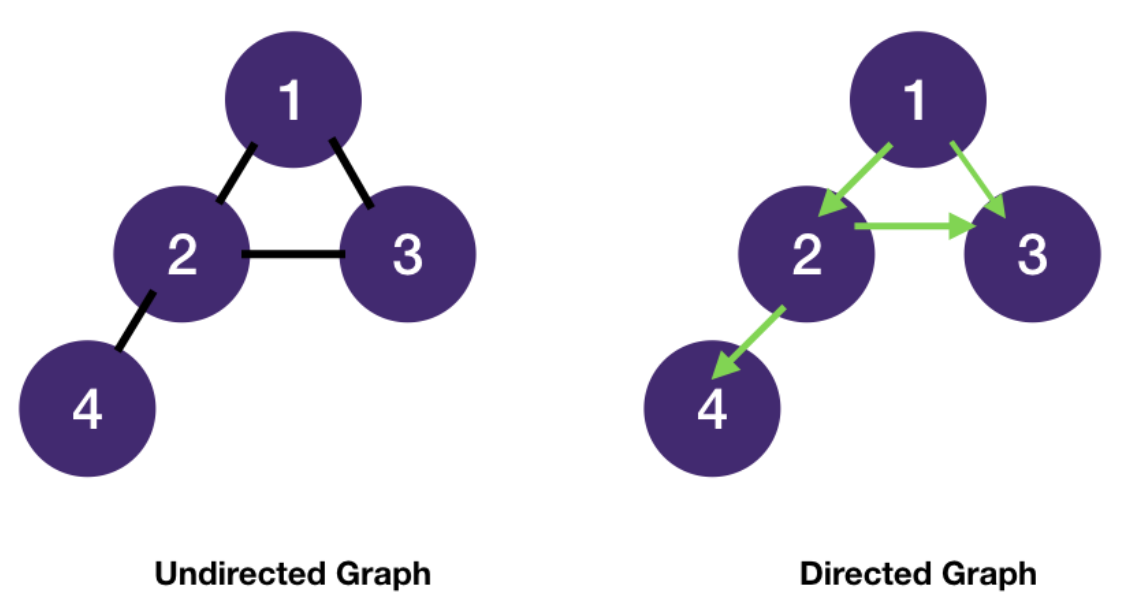
- Edges can be undirected or directed. For most interview problems we are dealing with undirected graphs.
- A tree is also an undirected graph.
- A path is a sequence of vertices.
- A cycle is a path that starts and ends at the same vertex.
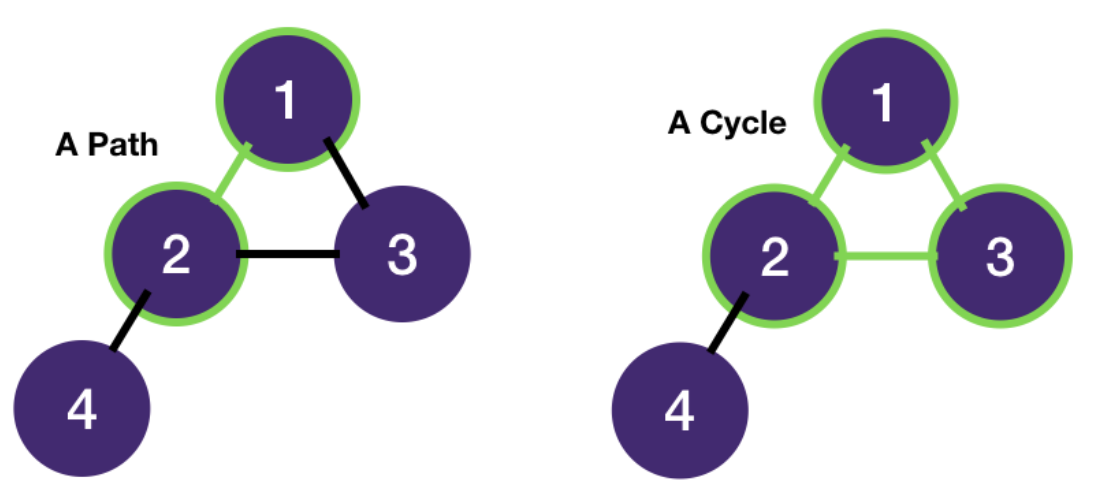
- An undirected graph is connected if every vertex is joined by a path to another vertex.
- Otherwise, it's disconnected.
- A graph is most commonly stored as a map of adjacency lists: for each vertex, store a list of its neighbors.
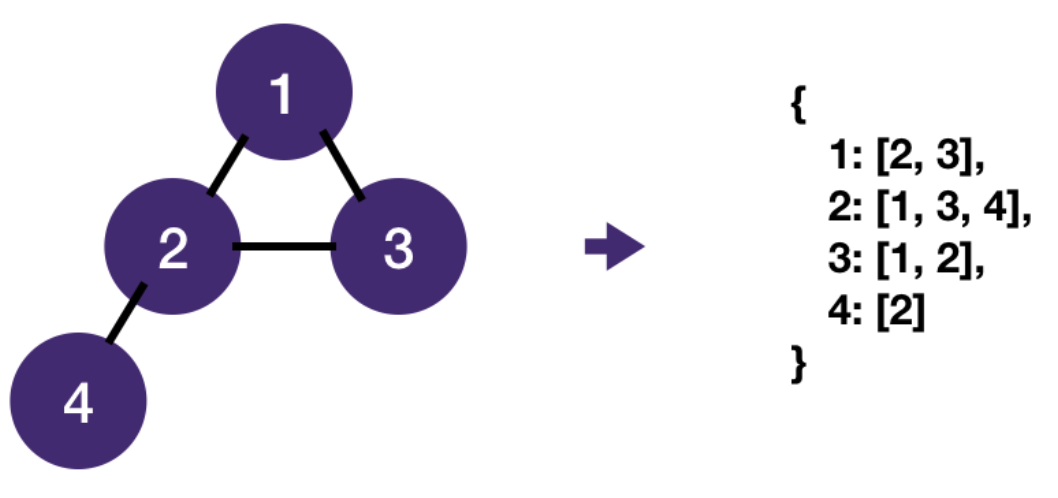
- Note that even though a graph is represented as an adjacency list , we don't actually have to create it upfront.
- What we really need is a function to get a vertex's neighbors.
Breadth First Search on Graphs
Tree vs Graph Traversal
- A Tree is a connected, acyclic undirected graph.
- Statistically, most interview graph problems are about connected and undirected graphs.
- So for simplicity, we're gonna define a tree as a graph without cycle.
- The search algorithms we have learned in tree modules are applicable to graphs as well.
- The difference between a tree and a graph is the possibility of having a cycle, we just have to handle this situation.
- We use an extra variable
visitedto keep track of vertices we have already visited to prevent re-visiting and getting into infinite loops. - visited can be any data structure that can answer existence queries quickly.
- For example, a hash set or an array where each element maps to a vertex in the graph can both do this in constant time.
- We use an extra variable
- Note minor terminology change from tree to graph - we call "children" "neighbors" since there's no parent-child relationship in a graph.
BFS on graphs
- Notice how the visited set prevents infinite loops. If we didn't have it, we would have enqueued 2's neighbors 1 and 3 into the queue again which would enqueue 2 again.
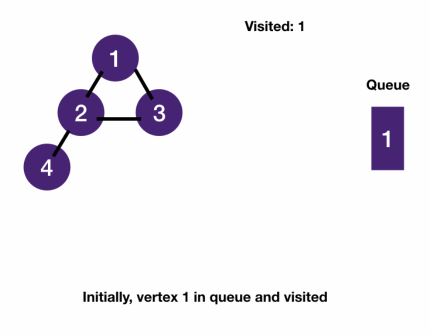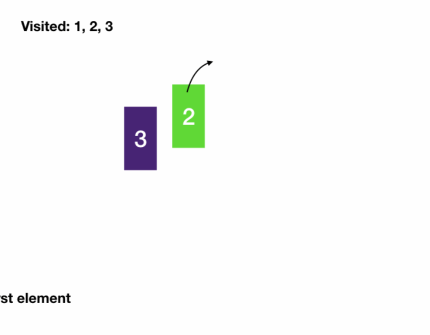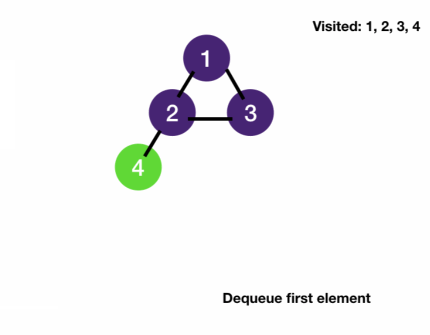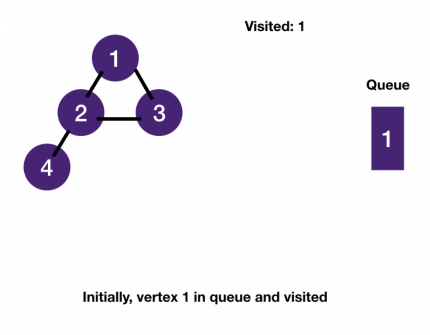
BFS on graph template
- BFS template consists of two core functions
- bfs: uses a queue to keep track of nodes to be visited
- get_neighbors: returns a node's neighbors.
- In an adjacency list representation, this would be returning the list of neighbors for the node.
- If the problem is about a matrix, this would be the surrounding valid cells as we will see in
number of islandsandknight shortest path - If the graph is implicit, we have to generate the neighbors as we traverse.
- We will see this in
word ladder
- BFS on tree
function bfsByQueue(root) {
const queue = [root];
while (queue.length > 0) {
const node = queue.shift();
for (const child of node.children) {
queue.push(child);
}
}
}
- BFS on graph
function getNeighbors(graph, node) {
return graph[node];
}
function bfs(root) {
const queue = [root];
const visisted = new Set();
while (queue.length > 0) {
const node = queue.shift();
for (const neighbor of getNeighbors(node)) {
if (visisted.has(neighbor)) continue;
queue.push(neighbor);
visisted.add(neighbor);
}
}
}
Tracking levels/Finding distance
- BFS is by-level traversal.
- Sometimes we need to track how many levels we have traversed (much like level order traversal problem in BFS on Tree module).
- Similar to binary tree level order traversal, we can get the number of nodes of a level from the queue size.
function bfsLevel(root) {
const queue = [root];
const visisted = new Set();
let level = 0;
while (queue.length > 0) {
const n = queue.length; // get # of nodes in the current level
for (let i=0; i<n; i++) {
const node = queue.shift();
for (const neighbor of getNeighbors(node)) {
if (visisted.has(neighbor)) continue;
queue.push(neighbor);
visisted.add(neighbor);
}
}
// increment level after we have processed all nodes of the level
level++;
}
}
When to use BFS?
Shortest path from A to B (unweight)- Graph of unknown or even infinite size, e.g.
knight shortest path Dijkstra Intro | Shortest Path in a Weighted Graph
Depth First Search on Graphs
- Similar to BFS, we just have to add visited to keep track of visited nodes and use get_neighbors to get the next nodes to visit.
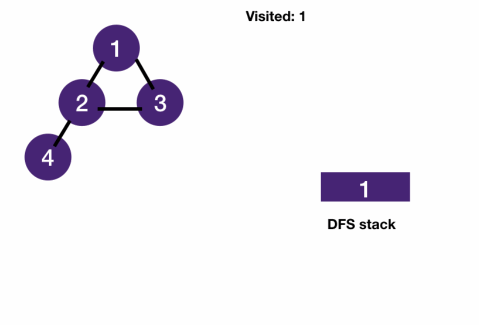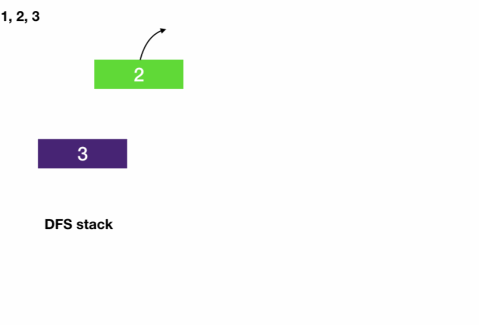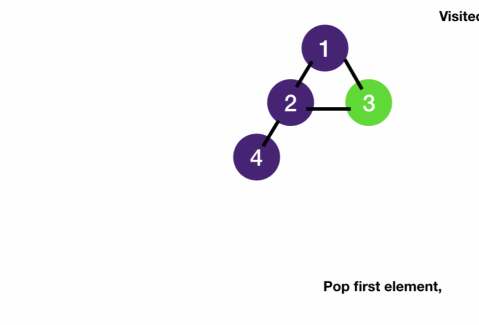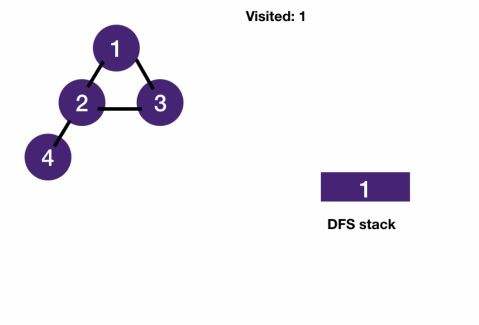
- DFS on tree
function dfs(root) {
if (!root) return;
for (const child of node.children) {
dfs(child);
}
}
- DFS on graph
function dfs(root, visited) {
for (const neighbor of getNeighbors(root)) {
if (visited.has(neighbor)) continue;
visited.add(neighbor);
dfs(neighbor, visited);
}
}
Complexity
- We only visit each vertex once in both BFS and DFS with visited.
- Since technically a graph is made of vertices and edges,
- the time complexity of BFS/DFS on graphs is normally expressed as
O(|V| + |E|)- where |V| stands for number of vertices and |E| stands for number of edges
- V is set of vertices and in math |V| means the size of a set
- the time complexity of BFS/DFS on graphs is normally expressed as
- Since technically a graph is made of vertices and edges,
BFS or DFS
When should you use one over the other?
- If you just have to visit each node once without memory constraints (e.g.
number of islandsproblem),- then it doesn't really matter which one you use.
- It comes down to your personal preference for recursion/stack vs queue.
| BFS is better at | DFS is better at |
|---|---|
| finding the shortest distance between two vertices | uses less memory than BFS for wide graphs, since BFS has to keep all the nodes in the queue, and for wide graphs this can be quite large. |
graph of unknown size, e.g. word ladder, or even infinite size, e.g. knight shortest path | finding nodes far away from the root, e.g. looking for an exit in a maze. |